draw tangent with curve civil 3d
3 Parametric Curves and Surfaces
This guide is an in-depth review of parametric curves with special focus on NURBS curves and the concepts of continuity and curvature.
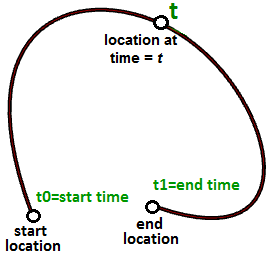
Suppose y'all travel every weekday from your business firm to your work. You get out at viii:00 in the morn and arrive at 9:00. At each bespeak in fourth dimension between 8:00 and ix:00, you lot would be at some location along the way. If you plot your location every infinitesimal during your trip, you tin define the path betwixt domicile and work past connecting the 60 points y'all plotted. Assuming you travel the exact same speed every day, at viii:00 you would exist at domicile (start location), at 9:00 you would be at work (finish location) and at 8:40 you would at the verbal same location on the path as the 40th plot point. Congratulations, you accept just divers your beginning parametric curve! You take used time as a parameter to define your path, and hence you lot tin phone call your path curve a parametric curve. The time interval you lot spend from starting time to end (8 to 9) is called the curve domain or interval.
In full general, we tin depict the \(x\), \(y\), and \(z\) location of a parametric curve in terms of some parameter \(t\) as follows:
\(x = x(t)\)
\(y = y(t)\)
\(z = z(t)\)
Where:
\(t\) is a range of existent numbers
We saw earlier that the parametric equation of a line in terms of parameter \(t\) is divers as:
\(x = 10' + t * a\)
\(y = y' + t * b\)
\(z = z' + t * c\)
Where:
\(x\), \(y\), and \(z\) are functions of t where t represents a range of existent numbers. \(x'\), \(y'\), and \(z'\) are the coordinates of a bespeak on the line segment. \(a\), \(b\), and \(c\) define the slope of the line, such that the vector \(\mathbf{\vec v} <a, b, c>\) is parallel to the line.

Nosotros tin can therefore write the parametric equation of a line segment using a \(t\) parameter that ranges betwixt two existent number values \(t0\), \(t1\) and a unit vector \(\mathbf{\vec v}\) that is in the direction of the line equally follows:
\(P = P' + t * \mathbf{\vec v}\)
Some other instance is a circle. The parametric equation of the circle on the xy-plane with a eye at the origin (0,0) and an angle parameter \(t\) ranging between \(0\) and \(2π\) radians is:

\(x = r \dot cos(t)\)
\(y = r \dot sin(t)\)
We can derive the general equation of a circle for the parametric i every bit follows:
\(x/r = cos(t)\)
\(y/r = sin(t)\)
And since:
\(cos(t)^2 + sin(t)^2 = 1\) (Pythagorean identity)
And then:
\((x/r)^2 + (y/r)^ii = 1\) , or
\(ten^2 + y^two = r^2\)
3.ane Parametric curves
Curve parameter
A parameter on a curve represents the address of a signal on that curve. Equally mentioned before, yous can retrieve of a parametric curve as a path traveled between two points in a sure amount of time, traveling at a fixed or variable speed. If traveling takes \(T\) corporeality of time, then the parameter t represents a time within \(T\) that translates to a location (point) on the curve.
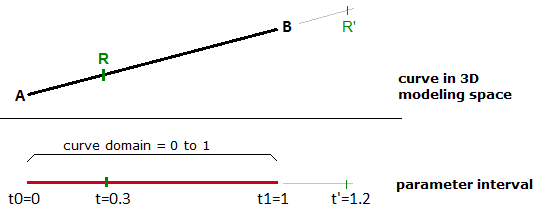
If you have a direct path (line segment) between the ii points \(A\) and \(B\), and \(\mathbf{\vec v}\) were a vector from \(A\) to \(B\) (\(\mathbf{\vec five} = B - A\)), and then yous tin can utilise the parametric line equation to find all points \(M\) betwixt \(A\) and \(B\) as follows:
\(One thousand = A + t*(B-A)\)
Where:
\(t\) is a value between 0 and ane.
The range of t values, 0 to 1 in this case, is referred to as the curve domain or interval. If t was a value outside the domain (less that 0 or more 1), and so the resulting indicate \(M\) will be outside the linear curve \(\overline{AB}\).
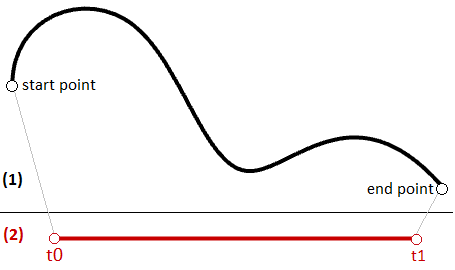
The same principle applies for whatever parametric bend. Any point on the curve can be calculated using the parameter t inside the interval or domain of values that define the limits of the curve. The start parameter of the domain is commonly referred to equally \(t0\) and the stop of the domain as \(t1\).
Bend domain or interval
A curve domain or interval is divers as the range of parameters that evaluate into a signal within that bend. The domain is unremarkably described with two real numbers defining the domain limits expressed in the form (min to max)or (min, max). The domain limits tin can be whatsoever two values that may or may not be related to the actual length of the curve. In an increasing domain, the domain min parameter evaluates to the commencement point of the bend and the domain max evaluates to the finish point ofthe curve.
Irresolute a curve domain is referred to as the procedure of reparameterizing the curve. For example, it is very mutual to alter the domain to exist (0 to ane). Reparameterizing a curve does not affect the shape of the 3-D curve. It is similar changing the travel fourth dimension on a path past running instead of walking, which does not change the shape of the path.
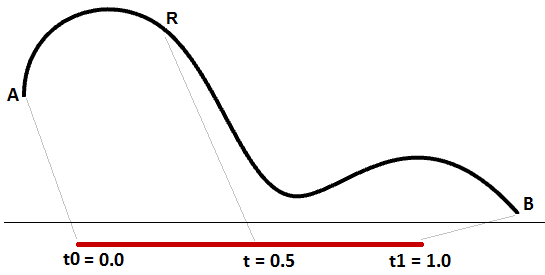
An increasing domain means that the minimum value of the domain points to the offset of the curve. Domains are typically increasing, but not always.
Curve evaluation
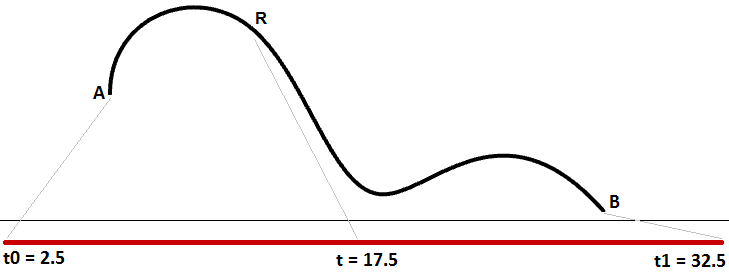
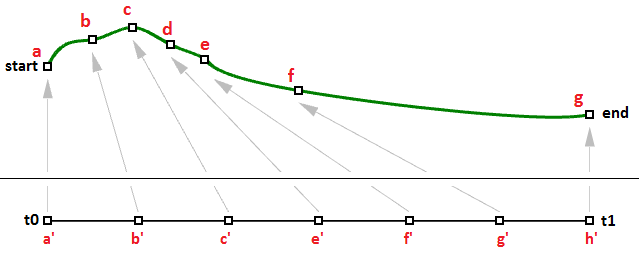
We learned that a curve interval is the range of all parameter values that evaluate to points within the 3-D bend. There is, still, no guarantee that evaluating at the middle of the domain, for instance, will requite a point that is in the center of the bend, as shown in Figure (29).
We tin can call back of uniform parameterization of a curve as traveling a path with constant speed. A degree-one line between two points is one case where equal intervals or parameters translate into equal intervals of arc length on the line. This is a special instance where equal intervals of parameters evaluate to equal intervals on the 3-D curve.
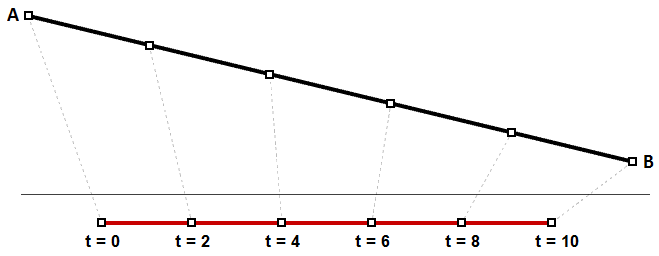
Information technology is, withal, more probable that the speed decreases or increases along the path. For example, if it takes 30 minutes to travel a route, it is unlikely that yous will be exactly half manner through at minute 15. Effigy (thirty) shows a typical case where equal parameter intervals evaluate to variable length on the 3-D curve.

You may need to evaluate points on a 3-D curve that are at a divers percentage of the curve length. For instance, you lot might demand to divide the curve into equal lengths. Typically, 3-D modelers provide tools to evaluate curves relative to arc length.
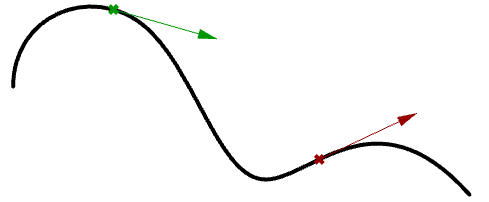
Tangent vector to a curve
A tangent to a curve at whatsoever parameter (or indicate on a curve) is the vector that touches the curve at that bespeak, simply does not cross over. The slope of the tangent vector equals the slope of the bend at the aforementioned bespeak. The following example evaluates the tangent to a curve at two different parameters.
Cubic polynomial curves
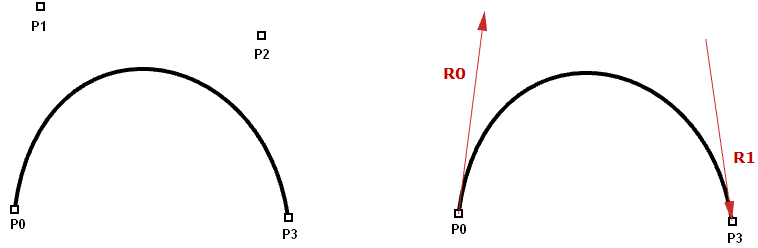
Hermite and Bézier curves are two examples of cubic polynomial curves that are determined by iv parameters. A Hermite curve is determined by two end points and 2 tangent vectors at these points, while a Bézier curve is defined by 4 points. While they differ mathematically, they share similar characteristics and limitations.
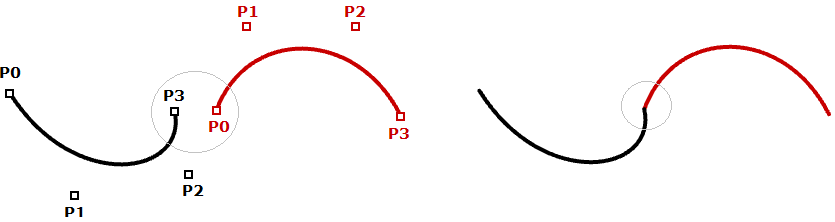
In virtually cases, curves are made out of multiple segments. This requires making what is called a piecewise cubic curve. Here is an illustration of a piecewise Bézier curve that uses seven storage points to create a 2-segment cubic curve. Note that although the terminal bend is joined, it does not look smooth or continuous.
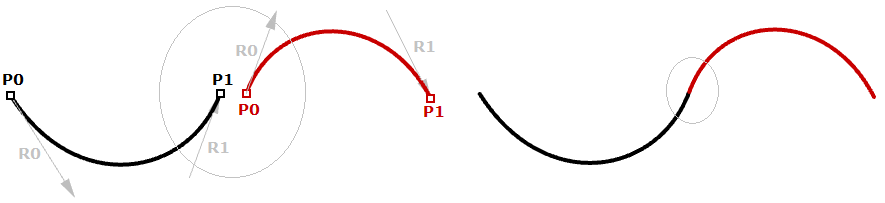
Although Hermite curves use the aforementioned number of parameters as Bézier curves (four parameters to define one curve), they offer the additional information of the tangent bend that can also exist shared with the next slice to create a smoother looking bend with less total storage, every bit shown in the following.
The non-uniform rational B-spline (NURBS) is a powerful bend representation that maintains even smoother and more continuous curves. Segments share more control points to achieve even smoother curves with less storage.
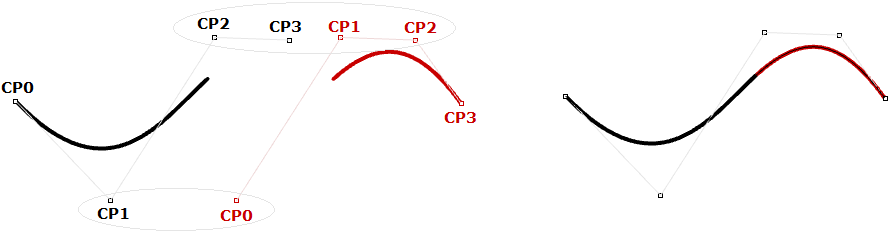
NURBS curves and surfaces are the main mathematical representation used by Rhinoceros to represent geometry. NURBS bend characteristics and components will exist covered with some particular later in this chapter.
Evaluating cubic Bézier curves
Named afterwards its inventor, Paul de Casteljau, the de Casteljau algorithm evaluates Bézier curves using a recursive method. The algorithm steps tin be summarized as follows:
Input:
Four points \(A\), \(B\), \(C\), \(D\) ascertain a curve \(t\), is any parameter within curve domain
Output:
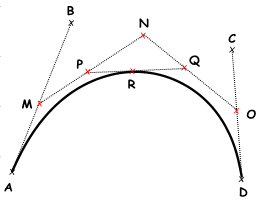
Point \(R\) on curve that is at parameter \(t\).
Solution:
- Observe point \(1000\) at \(t\) parameter on line \(\overline{AB}\).
ii.Find point \(North\) at \(t\) parameter on line \(\overline{BC}\).
3.Notice point \(O\) at \(t\) parameter on line \(\overline{CD}\).
iv.Find point \(P\) at \(t\) parameter on line \(\overline{MN}\).
5.Find indicate \(Q\) at \(t\) parameter on line \(\overline{NO}\).
6.Observe signal \(R\) at \(t\) parameter on line \(\overline{PQ}\).
3.2 NURBS curves
NURBS is an accurate mathematical representation of curves that is highly intuitive to edit. It is piece of cake to represent free-form curves using NURBS and the control structure makes it easy and predictable to edit.
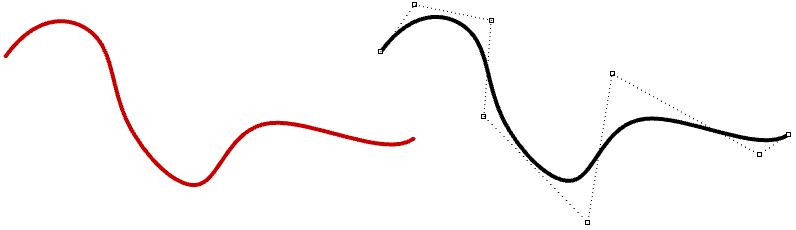
There are many books and references for those of you interested in an in-depth reading about NURBS. A basic agreement of NURBS is notwithstanding necessary to help employ a NURBS modeler more than finer. There are iv main attributes define the NURBS curve: caste, control points, knots, and evaluation rules.
- Wikipedia: De Boor's algorithm
- Michigan Tech, Department of Informatics, De Churl'due south algorithm
Degree
Curve caste is a whole positive number. Rhinoceros allows working with any degree bend starting with 1. Degrees one, 2, iii, and 5 are the near useful merely the degrees iv and those above v are not used much in the existent world. Post-obit are a few examples of curves and their degree:
Control points
The control points of a NURBS curve is a listing of at least (degree+1) points. The most intuitive mode to alter the shape of a NURBS bend is through moving its control points.
The number of command points that impact each span in a NURBS bend is defined past the degree of the curve. For example, each span in a degree-one curve is affected but by the 2 stop control points. In a degree-2 bend, three command points touch each bridge and so on.
Weights of control points
Each control point has an associated number called weight. With a few exceptions, weights are positive numbers. When all control points take the same weight, usually 1, the curve is called not-rational. Intuitively, you lot can think of weights every bit the corporeality of gravity each control indicate has. The college the relative weight a control point has, the closer the bend is pulled towards that control point.
It is worth noting that it is best to avoid changing curve weights. Changing weights rarely gives desired result while it introduces a lot of calculation challenges in operations such every bit intersections. The only good reason for using rational curves is to represent curves that cannot otherwise be fatigued, such as circles and ellipses.
Scaling a knot listing does not affect the 3D curve. If y'all change the domain of the curve in the above instance from "0 to 4" to "0 to one", knot listing get scaled, just the 3D curve does not change.

Knots
Each NURBS curve has a listing of numbers associated with it called a list of knots (sometimes referred to every bit knot vector). Knots are a little harder to understand and set. While using a 3-D modeler, you volition not need to manually set the knots for each curve you create; a few things volition be useful to learn about knots.
Knots are parameter values
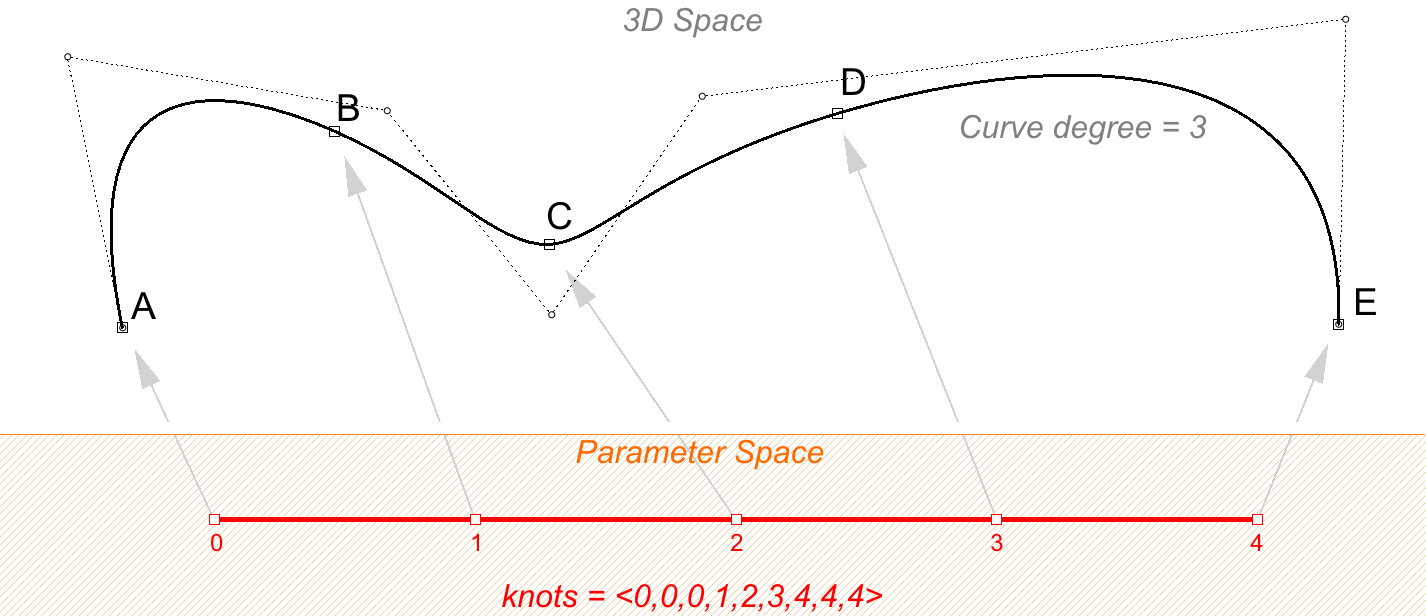
Knots are a not-decreasing list of parameter values that lie within the bend domain. In Rhinoceros, there is degree-i more knots than command points. That is the number of knots equals the number of control points plus bend degree minus 1:
Usually, for non-periodic curves, the first degree many knots are equal to the domain minimum, and the concluding degree many knots are equal to the domain maximum.
For example, the knots of an open degree-iii NURBS bend with 7 command points and a domain between 0 and 4 may look similar <0, 0, 0, ane, two, 3, iv, 4, iv>.
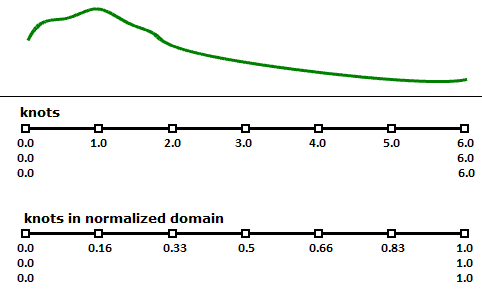
Knot multiplicity
The multiplicity of a knot is the number of times it is listed in the list of knots. The multiplicity of a knot cannot be more than the caste of the curve. Knot multiplicity is used to control continuity at the respective curve indicate.
Fully-multiple knots
A fully multiple knot has multiplicity equal to the curve degree. At a fully multiple knot there is a corresponding control point, and the bend goes through this point.
For example, clamped or open curves have knots with full multiplicity at the ends of the curve. This is why the end control points coincide with the curve end points. Interior fully multiple knots permit a kink in the curve at the corresponding point.
Unproblematic knot
A simple knot is one with value appearing only once. Interior knots are typically elementary.
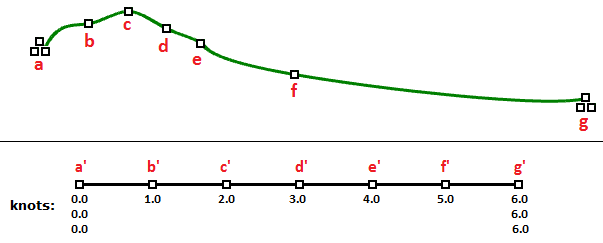
Uniform knots
A uniform list of knots satisfies the following status.
Knots start with a fully-multiple knot, are followed by simple knots, and terminate with a fully-multiple knot. The values are increasing and equally spaced. This is typical of clamped or open curves. Periodic curves work differently as we will see later.
Here are two curves that take the same number and location of control points, and still have different knots and curve shape:
| Degree = iii Number of control points = 7 knots = <0,0,0,one,2,3,4,4,4> = nine knots Domain (0 to iv) |  |
| Degree = three Number of control points = 7 knots = <0,0,0,i,1,one,four,4,4> = nine knots Domain (0 to 4) Note: A fully multiple knot in the heart creates a kink and the curve is forced to go through the associated control point. | 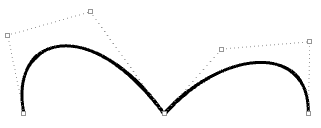 |
Evaluation rule
The evaluation rule uses a mathematical formula that takes a number within the curve domain and assigns a signal. The formula takes into account the degree, control points, and knots.
Using this formula, specialized curve functions can take a curve parameter and produce the corresponding point on that bend. A parameter is a number that lies within the curve domain. Domains are usually increasing and consist of ii numbers: the minimum domain parameter \(t(0)\) that evaluates to the start point of the bend and the maximum \(t(one)\) that evaluates to the end point of the curve.
Characteristics of NURBS curves
In club tocreate a NURBS bend, yous will need to provide the followinginformation:
- Dimension, typically iii
- Caste, (sometimes utilise the order,which is equal to caste+one)
- Control points (list of points)
- Weight of the control indicate (listof numbers)
- Knots (listing of numbers)
When you create a bend, y'all need to at least define the degree and locations of the control points. The remainder of the information necessary to construct NURBS curves tin be generated automatically. Selecting an cease point to coincide with the start point would typically create a periodic smoothen closed curve. The post-obit table shows examples of open and closed curves:
| Degree-one open curve. The curve goes through all control points. |  |
| Degree-three open up curve. Both curve ends coincide with end control points. |  |
| Degree-iii closed periodic curve. The curve seam does not become through a command bespeak. | 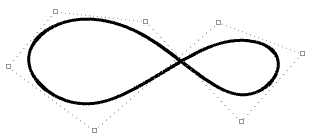 |
| Moving control points of a periodic curve does non touch curve smoothness. | 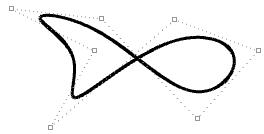 |
| Kinks are created when the curve is forced through some command points. | 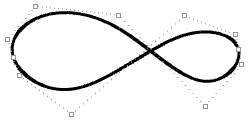 |
| Moving the control points of a not-periodic curve does non guarantee smoothen continuity of the curve, simply enables more control over the result. | 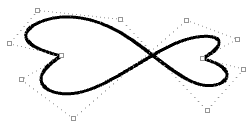 |
Clamped vs. periodic NURBS curves
The terminate points of airtight clamped curves coincide with end command points. Periodic curves are polish airtight curves. The best fashion to understand the differences betwixt the two is through comparing control points and knots.
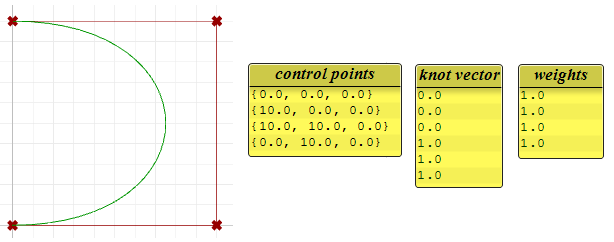
The post-obit is an case of an open up, clamped non-rational NURBS curve. This bend has iv command points, uniform knots with full-multiplicity at the starting time and stop knots and the weights of all command points equal to 1.

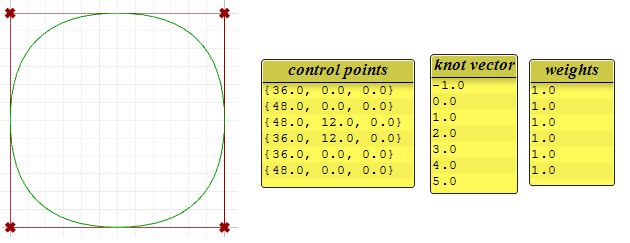
The following circular bend is an example of a degree-3 closed periodic NURBS curve. It is likewise non-rational considering all weights are equal. Note that periodic curves require more than control points with few overlapping. Also the knots are simple.
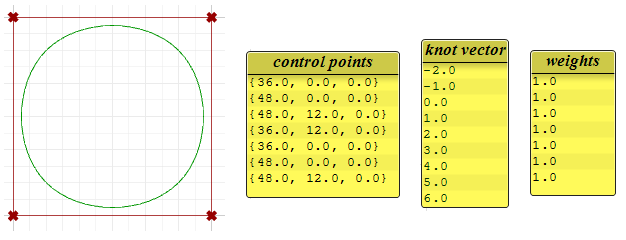
Notice that the periodic curve turned the 4 input points into 7 command points (degree+4), while the clamped curve used only the iv control points. The knots of the periodic curve uses merely uncomplicated knots, while the clamped curve start and stop knots have full multiplicity forcing the bend to get through the kickoff and end control points.
If we set up the degree of the previous examples to 2 instead of 3, the knots become smaller, and the number of control points of periodic curves changes.

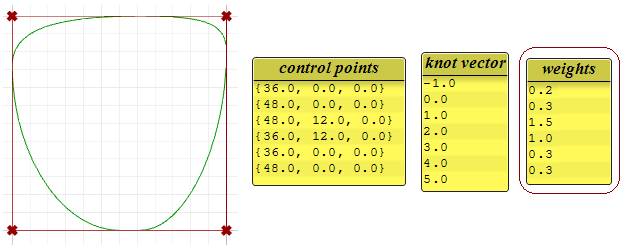
Weights
Weights of control points in a uniform NURBS curve are set to ane, merely this number can vary in rational NURBS curves. The following example shows the result of varying the weights of control points.
Evaluating NURBS curves
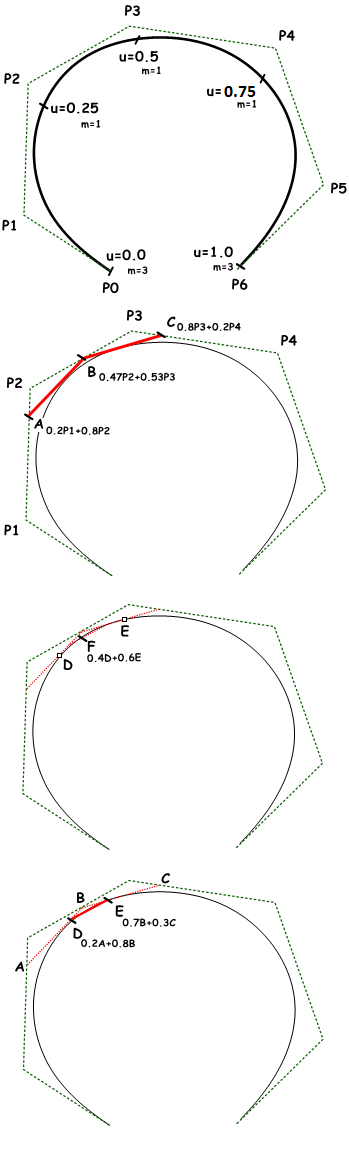
Named after its inventor, Carl de Boor, the de Churl'south algorithmi is a generalization of the de Casteljau algorithm for Bézier curves. Information technology is numerically stable and is widely used to evaluate points on NURBS curves in 3-D applications. The following is an example for evaluating a indicate on a degree-3 NURBS curve using de Boor'southward algorithm.
Input:
7 control points \(P0\) to \(P6\)
Knots:
\(u_0 = 0.0\)
\(u_1 = 0.0\)
\(u_2 = 0.0\)
\(u_3= 0.25\)
\(u_4 = 0.v\)
\(u_5 = 0.75\)
\(u_6 = i.0\)
\(u_7 = i.0\)
\(u_8 = one.0\)
Output:
Point on curve that is at \(u=0.4\)
Solution:
1. Calculate coefficients for the first iteration:
\(A_c = ((u – u_1)/(u_{one+iii} – u_1) = 0.eight\)
\(B_c = (u – u_2)/(u_{2+3} – u_2) = 0.53\)
\(C_c = (u – u_3)/(u_{3+3} – u_3) = 0.2\)
ii. Calculate points using coefficient information:
\(A = 0.2P_1 + 0.8P_2\)
\(B = 0.47 P_2 + 0.53 P_3\)
\(C = 0.eight P_3 + 0.2 P_4\)
3. Summate coefficients for the 2d iteration:
\(D_c = (u – u_2) / (u_{ii+three-1} – u_2) = 0.viii\)
\(E_c = (u – u_3) / (u_{3+iii-one} – u_3) = 0.3\)
4. Calculate points using coefficient information:
\(D = 0.2A+ 0.8B\)
\(E = 0.7B + 0.3C\)
five. Calculate the terminal coefficient:
\(Fc = (u – u_3)/ (u_{3+3-ii} – u_3) = 0.6\)
Find the signal on bend at \(u=0.4\) parameter:
\(F= 0.4D + 0.6E\)
three.3 Curve geometric continuity
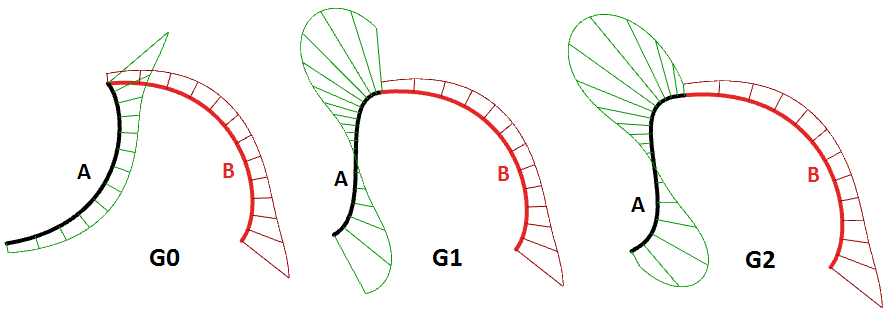
Continuity is an important concept in 3‑D modeling. Continuity is important for achieving visual smoothness and for obtaining smooth low-cal and airflow. The following table shows diverse continuities and their definitions:
| G0 | (Position continuous) | Two curve segments joined together |
| G1 | (Tangent continuous) | Direction of tangent at joint point is the same for both curve segments. |
| G2 | ( Curvature Continuous) | Curvatures likewise as tangents agree for both curve segments at the common endpoint. |
| GN | ……. | The curves agree to higher club |
3.4 Bend curvature
Curvature is a widely used concept in modeling 3‑D curves and surfaces. Curvature is defined every bit the change in inclination of a tangent to a curve over unit length of arc. For a circle or sphere, it is the reciprocal of the radius and information technology is constant across the full domain.
At any point on a curve in the plane, the line best approximating the curve that passes through this indicate is the tangent line. We tin too detect the best approximating circle that passes through this indicate and is tangent to the bend. The reciprocal of the radius of this circle is the curvature of the curve at this point.
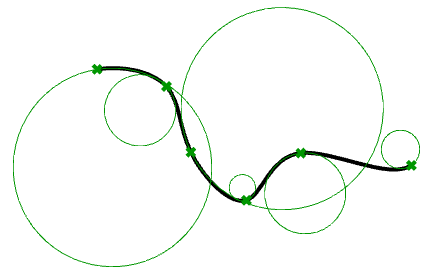
The best approximating circle can lie either to the left or to the right of the bend. If nosotros care about this, nosotros establish a convention, such as giving the curvature positive sign if the circle lies to the left and negative sign if the circle lies to the correct of the bend. This is known as signed curvature. Curvature values of joined curves indicate continuity betwixt these curves.
iii.5 Parametric surfaces
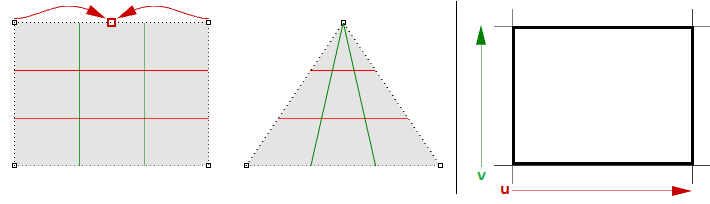
Surface parameters
A parametric surface is a function of two independent parameters (usually denoted \(u\), \(v\)) over some two-dimensional domain. Take for example a plane. If we have a bespeak \(P\) on the plane and two nonparallel vectors on the plane, \(\vec a\) and \(\vec b\), then we can ascertain a parametric equation of the airplane in terms of the ii parameters \(u\) and \(v\) as follows:
\(P = P' + u * \mathbf{\vec a} + five * \mathbf{\vec b}\)
Where:
\(P'\): is a known point on the plane
\(\mathbf{\vec a}\): is the showtime vector on the airplane
\(\mathbf{\vec b}\): is the first vector on the aeroplane
\(u\): is the offset parameter
\(v\): is the showtime parameter

Another instance is the sphere. The Cartesian equation of a sphere centered at the origin with radius \(R\) is
\(x^2 + y^2 + z^2 = R^2\)
That means for each bespeak, there are three variables (\(x\), \(y\), \(z\)), which is not useful to employ for a parametric representation that requires but 2 variables. However, in the spherical coordinate organization, each point is found using the iii values:
\(r\): radial altitude betwixt the signal and the origin
\(θ\): the bending from the ten-axis in the xy-aeroplane
\(ø\): the angle from the z-axis and the point
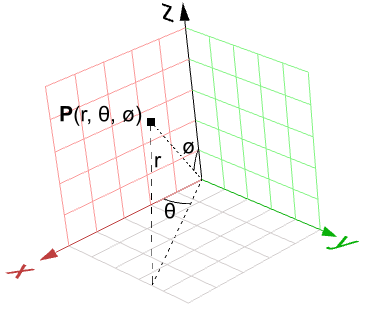
A conversion of points from spherical to Cartesian coordinate tin be obtained every bit follows:
\(x = r * sin(ø) * cos(θ)\)
\(y = r * sin(ø) * sin(θ)\)
\(z = r * cos (ø)\)
Where:
\(r\) is distance from origin \(≥ 0\)
\(θ\) is running from \(0\) to \(2π\)
\(ø\) is running from \(0\) to \(π\)
Since \(r\) is constant in a sphere surface, we are left with merely two variables, and hence nosotros can use the in a higher place to create a parametric representation of a sphere surface:
\(u = θ\)
\(five = ø\)
So that:
\(ten = r * sin(v) * cos(u)\)
\(y = r * sin(v) * sin(u)\)
\(z = r * cos(v)\)
Where (\(u\), \(v\)) is inside the domain (\(2 π\), \(π\))

The parametric surface follows the general class:
\(x = 10(u,v)\)
\(y = y(u,v)\)
\(z = z(u,v)\)
Where:
\(u\) and \(5\) are the 2 parameters within the surface domain or region.
Surface domain
A surface domain is defined every bit therange of (\(u,v\)) parameters that evaluate into a iii D indicate on thatsurface. The domain in each dimension (\(u\) or \(v\)) is usually describedas two existent numbers (\(u_{min}\) to \(u_{max}\)) and (\(v_{min}\) to \(v_{max}\))
Changing a surface domain is referredto as reparameterizing the surface. An increasingdomain ways that the minimum value of the domain points to theminimum point of the surface. Domains are typically increasing, butnot always.

Surface evaluation
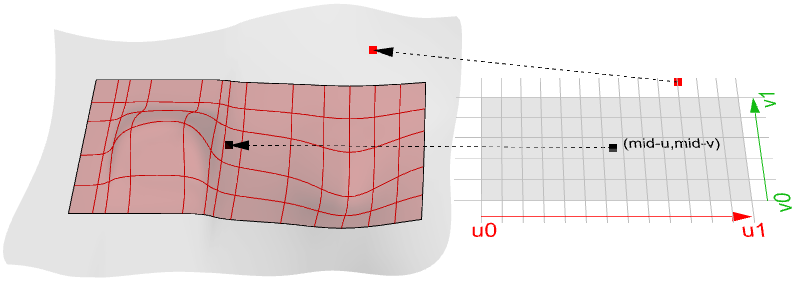
Evaluating a surface at a parameter that is inside the surface domain results in a point that is on the surface. Keep in listen that the middle of the domain (\(u_{mid}\), \(v_{mid}\)) might non necessarily evaluate to the middle signal of the 3-D surface. Also, evaluating \(u-\) and \(five-\) values that are outside the surface domain will not give a useful result.
Tangent airplane of a surface
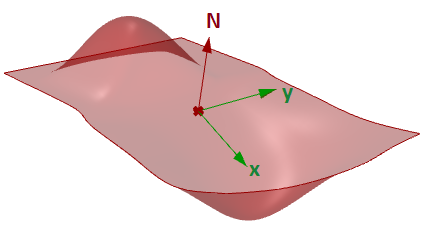
The tangent aeroplane to a surface at a given point is the plane that touches the surface at that point. The z-direction of the tangent plane represents the normal direction of the surface at that point.
3.6 Surface geometric continuity
Many models cannot be constructed from i surface patch. Continuity between joined surface patches is important for visual smoothness, low-cal reflection, and airflow. The following table shows various continuities and their definitions:
| G0 | (Position continuous) | Two surfaces joined together. |
| G1 | (Tangent continuous) | The corresponding tangents of the ii surfaces along their joint edge are parallel in both u‑ and v‑directions. |
| G2 | ( Curvature Continuous) | Curvatures as well every bit tangents agree for both surfaces at the mutual edge. |
| GN | ……. | The surfaces hold to college social club. |
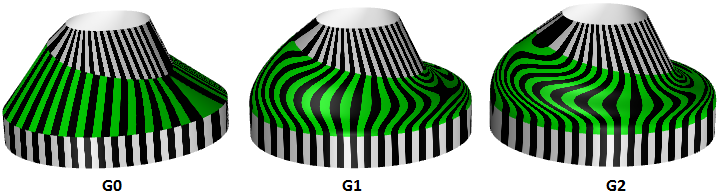
3.7 Surface curvature
For surfaces, normal curvature is one generalization of curvature to surfaces. Given a signal on the surface and a direction lying in the tangent aeroplane of the surface at that point, the normal section curvature is computed past intersecting the surface with the plane spanned by the point, the normal to the surface at that betoken, and the management. The normal section curvature is the signed curvature of this curve at the point of interest.
If we look at all directions in the tangent plane to the surface at our point, and we compute the normal curvature in all these directions, there will be a maximum value and a minimum value.
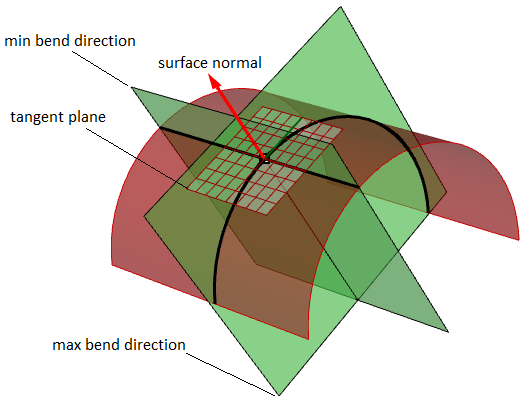
Principal curvatures
The principal curvatures of a surface at a signal are the minimum and maximum of the normal curvatures at that point. They measure the maximum and minimum bend amount of the surface at that point. The principal curvatures are used to compute the Gaussian and hateful curvatures of the surface.
For instance, in a cylindrical surface, there is no bend forth the linear direction (curvature equals zero) while the maximum bend is when intersecting with a aeroplane parallel to the terminate faces (curvature equals ane/radius). Those ii extremes make the principle curvatures of that surface.
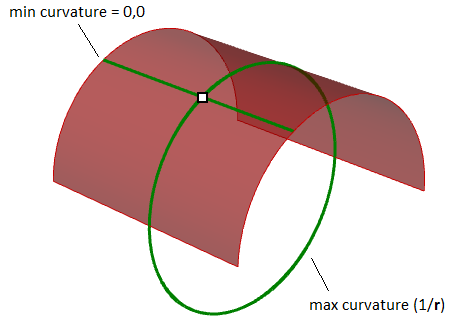
Gaussian curvature
The Gaussian curvature of a surface at a point is the product of the master curvatures at that indicate. The tangent aeroplane of any betoken with positive Gaussian curvature touches the surface locally at a single point, whereas the tangent plane of any betoken with negative Gaussian curvature cuts the surface.

A: Positive curvature when surface is bowl-like.
B: Negative curvature when surface is saddle-like.
C: Zero curvature when surface is flat in at least ane direction (airplane, cylinder).

Hateful curvature
The mean curvature of a surface at a point is 1-one-half of the sums of the principal curvatures at that point. Whatever betoken with zero mean curvature has negative or nothing Gaussian curvature.
Surfaces with zero mean curvature everywhere are minimal surfaces. Physical processes which can exist modeled past minimal surfaces include the formation of lather films spanning fixed objects, such every bit wire loops. A soap film is not distorted by air pressure (which is equal on both sides) and is free to minimize its expanse. This contrasts with a soap bubble, which encloses a fixed quantity of air and has unequal pressures on its inside and exterior. Hateful curvature is useful for finding areas of precipitous change in the surface curvature.
Surfaces with constant mean curvature everywhere are often referred to as constant mean curvature (CMC) surfaces. CMC surfaces include the germination of soap bubbles, both complimentary and attached to objects. A lather chimera, unlike a uncomplicated soap flick, encloses a volume and exists in equilibrium where slightly greater pressure inside the bubble is balanced by the area-minimizing forces of the chimera itself.
three.8 NURBS surfaces
You lot can think of NURBS surfaces as a grid of NURBS curves that go in two directions. The shape of a NURBS surface is defined by a number of control points and the degree of that surface in each one of the 2 directions (u- and v-directions). NURBS surfaces are efficient for storing and representing complimentary-form surfaces with a loftier degree of accuracy. The mathematical equations and details of NURBS surfaces are beyond the scope of this text. We volition only focus on the characteristics that are most useful for designers.
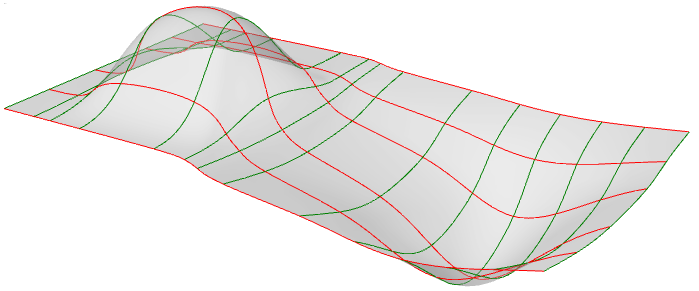
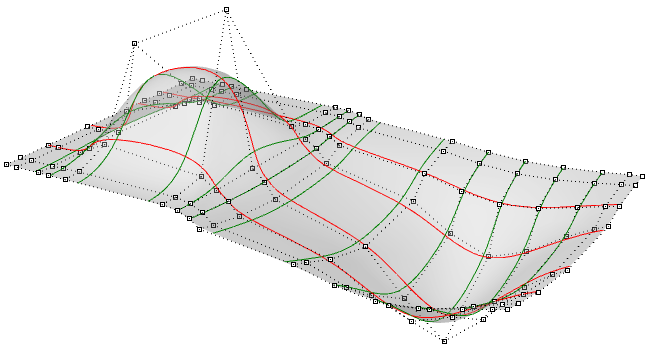
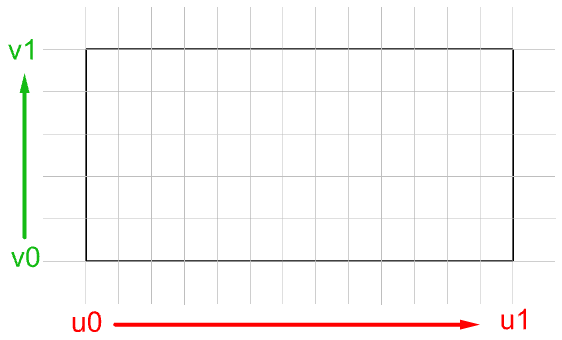
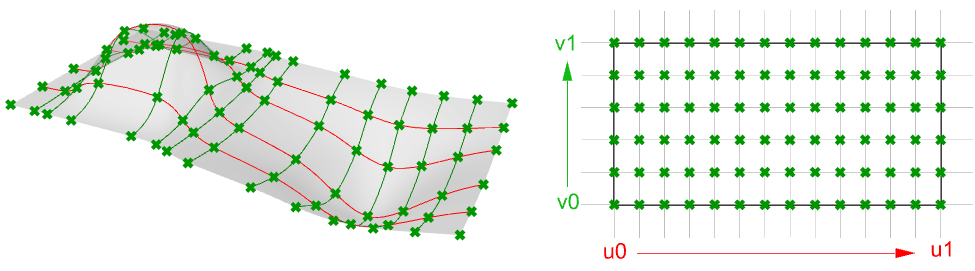
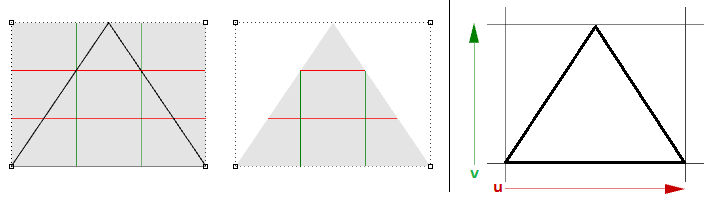
Evaluating parameters at equal intervals in the 2-D parameter rectangle does not translate into equal intervals in 3-D space in about cases.
Characteristics of NURBS surfaces
NURBS surface characteristics are very like to NURBS curves except there is one additional parameter. NURBS surfaces concord the following data:
- Dimension, typically 3
- Caste in u‑and five‑directions: (sometimes use gild which is degree + i)
- Control points (points)
- Weights of control points (numbers)
- Knots (numbers)
As with the NURBS curves, you will probably not demand to know the details of how to create a NURBS surface, since 3-D modelers will typically provide good set of tools for this. You can always rebuild surfaces (and curves for that thing) to a new degree and number of command points. Surface can be open up, closed, or periodic. Here are few examples of surfaces:
| Caste-1 surface in both u- and v-directions. All control points lie on the surface. | 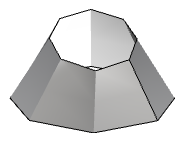 |
| Degree-3 in the u-direction and degree‑1 in the v-management open surface. The surface corners coincide with corner command points. |  |
| Degree-3 in the u-direction and degree 1 in the five-direction closed (non-periodic) surface. Some control points coincide with the surface seam. |  |
| Moving control points of a closed (non-periodic) surface causes a kink and the surface does not look smooth. | 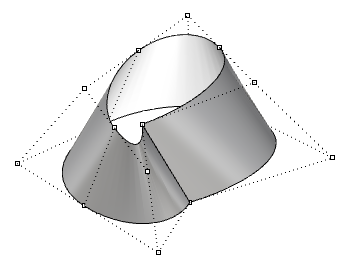 |
| Degree 3 the u-direction and caste 1 in the v-direction periodic surface. The surface control points practice not coincide with the surface seam. | 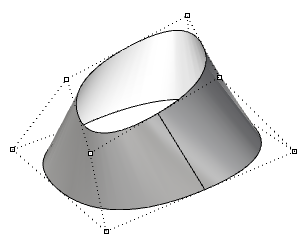 |
| Moving the control points of a periodic surface does not touch surface smoothness or create kinks. | 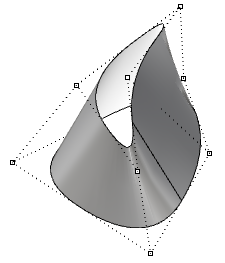 |
Singularity in NURBS surfaces
For example, if you lot take a linear edge of a simple plane, and you drag the two cease control points of an edge then they overlap (collapse) at the heart, you will get a atypical edge. You lot will notice that the surface isocurves converge at the singular signal.
The above triangular shape can be created without singularity. You can trim a surface with a triangle polyline. When yous examine the underlying NURBS construction, you run across that information technology remains a rectangular shape.
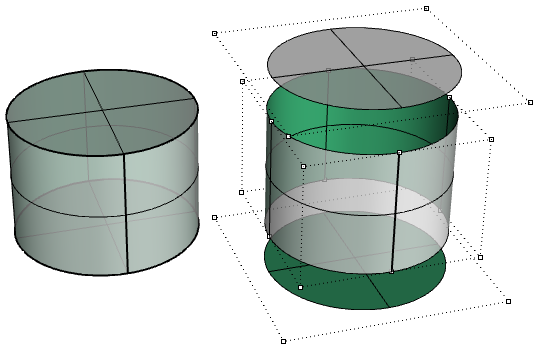
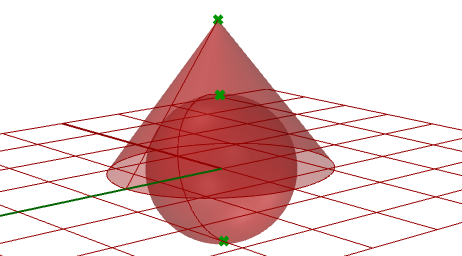
Other mutual examples of surfaces that are hard to generate without singularity are the cone and the sphere. The top of a cone and top and bottom edges of a sphere are collapsed into i point. Whether there is singularity or not, the parameter rectangle maintains a more or less rectangular region.
Trimmed NURBS surfaces
NURBS surfaces can exist trimmed or untrimmed. Trimmed surfaces use an underlying NURBS surface and closed curves to trim out part of that surface. Each surface has one closed curve that defines the outer border (outer loop) and can take non-intersecting closed inner curves to ascertain holes (inner loops). A surface with an outer loop that is the same equally that of its underlying NURBS surface and that has no holes is what nosotros refer to every bit an untrimmed surface.

3.nine Polysurfaces
A polysurface consists of two or more(possibly trimmed) NURBS surfaces joined together. Each surface hasits own construction, parameterization, and isocurve directions that donot accept to match. Polysurfaces are represented using the boundaryrepresentation (BRep). The BRep structure describes surfaces,edges, and vertices with trimming information and connectivity amongdifferent parts. Trimmed surface are also represented using BRep datastructure.

The BRep is a information structure that describes each face in terms of its underlying surface, surrounding 3-D edges, vertices, parameter space ii-D trims, and relationship between neighboring faces. BRep objects are also chosen solids when they are airtight (watertight).
An example polysurface is a simple box that is made out of six untrimmed surfaces joined together.

The same box tin be made using trimmed surfaces, such as the elevation ane in the post-obit example.

The top and bottom faces of the cylinder in the post-obit example are trimmed from planar surfaces.
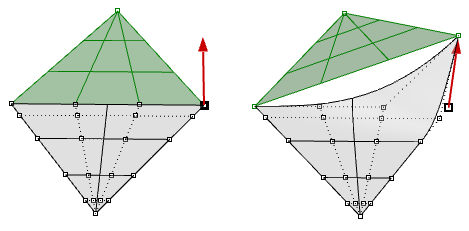
We saw that editing NURBS curves and untrimmed surfaces is intuitive and can be done interactively by moving control points. Still, editing trimmed surfaces and polysurfaces can be challenging. The principal claiming is to be able to maintain joined edges of dissimilar faces within the desired tolerance. Neighboring faces that share common edges can be trimmed and exercise non commonly take matching NURBS construction, and therefore modifying the object in a manner that deforms that common border might event in a gap.
Another challenge is that in that location is typically less control over the effect, particularly when modifying trimmed geometry.
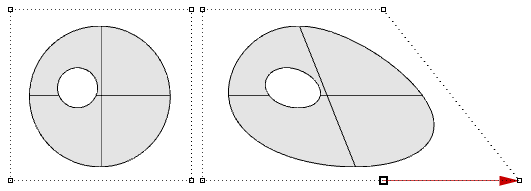
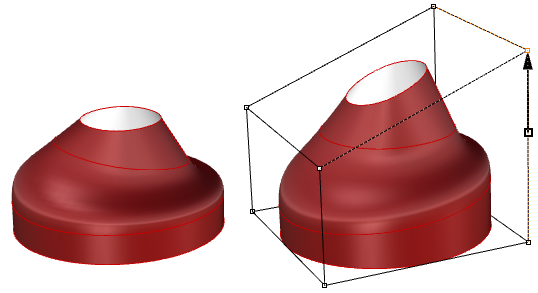
Trimmed surfaces are described in parameter infinite using the untrimmed underlying surface combined with the 2-D trim curves that evaluate to the 3-D edges within the 3-D surface.
3.10 Tutorials
The following tutorials use the concepts learned in this affiliate. They use Rhinoceros 5 and Grasshopper 0.9.
iii.10.1 Continuity betwixt curves
Examine the continuity between two input curves. Continuity assumes that the curves meet at the end of the offset curve and the first of the second curve.

Input:
2 input curves.
Parameters:
Calculate the following to be able to make up one's mind the continuity between ii curves:
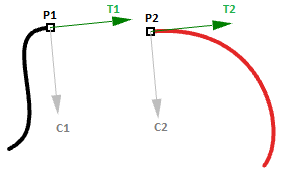
- The finish point of the offset bend (\(P1\))
- The start bespeak of the 2nd bend (\(P2\))
- The tangent at the finish of the first curve and at the start of the 2nd curve (\(T1\) and \(T2\)).
- The curvature at the cease of the first bend and at the starting time of the 2d bend (\(C1\) and \(C2\)).
Solution:
one. Reparameterize the input curves. We do that so that we know that the start of the curve evaluates at \(t=0\) and the end at \(t=1\).
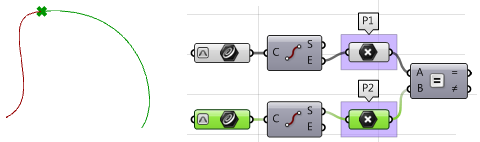
2. Extract the end and showtime points of the two curves, and check whether they coincide. If they practice, the two curves are at to the lowest degree \(G0\) continuous.
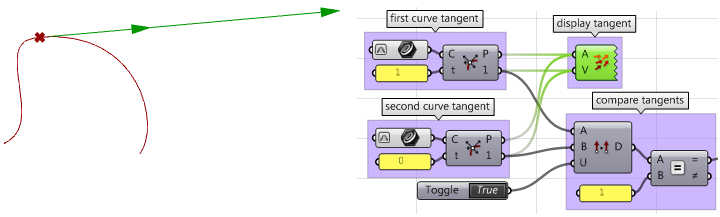
3. Calculate tangents.
iv. Compare the tangents using the dot product. Make certain to unitize vectors. If the curves are parallel, then nosotros have at to the lowest degree \(G1\) continuity.
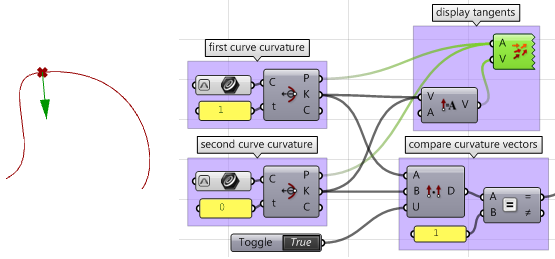
5. Calculate curvature vectors.
6. Compare curvature vectors, and if they agree, the two curves are \(G2\) continuous.
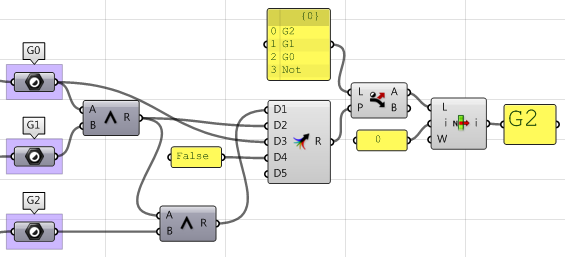
seven. Create logic that filters through the iii results (G1, G2, and G3) and select the highest continuity.
Using the Grasshopper VBScript component:
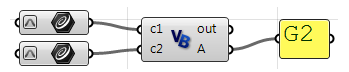
Individual Sub RunScript(ByVal c1 As Curve, ByVal c2 As Curve, ByRef A Equally Object) 'declare variables Dim continuity Every bit New Cord("") Dim t1, t2 As Double Dim v_c1, v_c2, c_c1, c_c2 As Vector3d 'extract commencement and cease points Dim end_c1 = c1.PointAtEnd Dim start_c2 = c2.PointAtStart 'bank check G0 continuity If end_c1.DistanceTo(start_c2) = 0 Then continuity = "G0" Stop If 'bank check G1 continuity If continuity = "G0" So 'calculate tangents v_c1 = c1.TangentAtEnd v_c2 = c2.TangentAtStart 'unitize tangent vectors v_c1.Unitize v_c2.Unitize 'compare tangents If v_c1 * v_c2 = 1.0 And so continuity = "G1" Terminate If Stop If 'check G2 continuity If continuity = "G1" Then 'extract the parameter at first and finish of the curves domain t1 = c1.Domain.Max t2 = c2.Domain.Min 'calculate curvature c_c1 = c1.CurvatureAt(t1) c_c2 = c2.CurvatureAt(t2) 'unitize curvature vectors c_c1.Unitize c_c2.Unitize 'compare vectors If c_c1 * c_c2 = 1.0 Then continuity = "G2" Terminate If Cease If 'Assign output A = continuity End Sub Using the Grasshopper Python component:
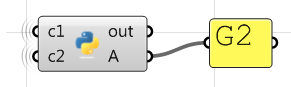
#decclare variables continuity = "" #extract start and stop points end_c1 = c1.PointAtEnd start_c2 = c2.PointAtStart #check G0 continuity if end_c1.DistanceTo(start_c2) == 0: continuity = "G0" #check G1 continuity if continuity == "G0": #calculate tangents v_c1 = c1.TangentAtEnd v_c2 = c2.TangentAtStart #unitize tangent vectors v_c1.Unitize() v_c2.Unitize() #compare tangents dot = v_c1 * v_c2 if dot == 1.0: continuity = "G1" else: print("Failed G1") impress(dot) #bank check G2 continuity if continuity == "G1": #extract the parameter at start and end of the curves domain t1 = c1.Domain.Max t2 = c2.Domain.Min #calculate curvature c_c1 = c1.CurvatureAt(t1) c_c2 = c2.CurvatureAt(t2) #unitize curvature vectors c_c1.Unitize() c_c2.Unitize() #compare vectors dot = c_c1 * c_c2 if dot == one.0: continuity = "G2" else: print("Failed G2") print(dot) #assign output A = continuity Using the Grasshopper C# component:
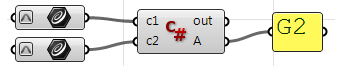
Private Sub RunScript(ByVal c1 As Curve, ByVal c2 As Bend, ByRef A Equally Object) 'declare variables Dim continuity As New Cord("") Dim t1, t2 As Double Dim v_c1, v_c2, c_c1, c_c2 Equally Vector3d 'extract start and end points Dim end_c1 = c1.PointAtEnd Dim start_c2 = c2.PointAtStart 'check G0 continuity If end_c1.DistanceTo(start_c2) = 0 Then continuity = "G0" End If 'check G1 continuity If continuity = "G0" And so 'calculate tangents v_c1 = c1.TangentAtEnd v_c2 = c2.TangentAtStart 'unitize tangent vectors v_c1.Unitize v_c2.Unitize 'compare tangents If v_c1 * v_c2 = 1.0 And so continuity = "G1" Cease If End If 'check G2 continuity If continuity = "G1" Then 'extract the parameter at commencement and end of the curves domain t1 = c1.Domain.Max t2 = c2.Domain.Min 'calculate curvature c_c1 = c1.CurvatureAt(t1) c_c2 = c2.CurvatureAt(t2) 'unitize curvature vectors c_c1.Unitize c_c2.Unitize 'compare vectors If c_c1 * c_c2 = 1.0 Then continuity = "G2" End If Finish If 'Assign output A = continuity End Sub iii.x.2 Surfaces with singularity
Excerpt atypical points in a sphere and a cone.
Input:
One sphere and one cone.
Parameters:
Singularity can be detected through analyzing the ii-D parameter space trims that have invalid or naught-length corresponding edges. Those trims ought to be singular.
Solution:
- Traverse through all trims in the input.
- Check if any trim has an invalid border and flag information technology as a singular trim.
- Extract signal locations in 3-D space.
Using the Grasshopper VB component:
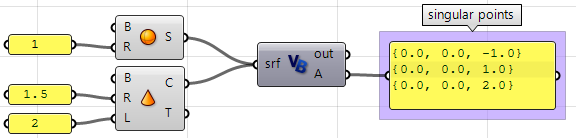
Private Sub RunScript(ByVal srf Every bit Brep, ByRef A Equally Object) 'Decalre a new list of points Dim singular_points As New List( Of Point3d) 'Examine all trims in the input For Each trim Equally BrepTrim In srf.Trims 'Null edge of a trim indicates a singularity If trim.Edge Is Nothing Then 'Notice the second parameter space point of the start or end of the trim Dim pt2d = New Point2d(trim.PointAtStart) 'Evaluate trim end point on the object surface Dim pt3d = trim.Face.PointAt(pt2d.x, pt2d.y) 'Add 3D point to the list of singular points singular_points.Add together(pt3d) End If Next 'Asign output A = singular_points Terminate Sub Using the Grasshopper Python component:
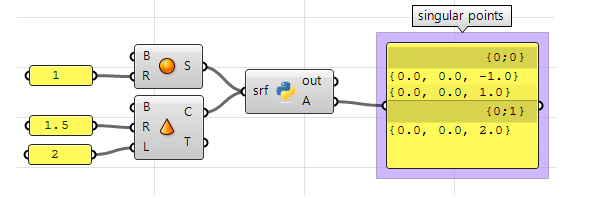
#Decalre a new list of points singular_points = [] #Examine all trims in the input brep for trim in srf.Trims: #Null edge of a trim indicates a singularity if trim.Border == None: #Find the 2nd parameter space betoken at trim start or finish pt2d = trim.PointAtStart #Evaluate trim end point on the object surface pt3d = trim.Face up.PointAt(pt2d.X, pt2d.Y) #Add 3D point to the list of singular points singular_points.append(pt3d) #Asign output A = singular_points Using the Grasshopper C# component:
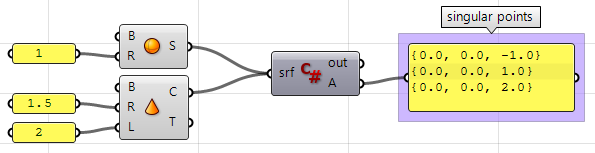
private void RunScript(Brep srf, ref object A) { //Decalre a new list of points List < Point3d > singular_points = new List<Point3d>(); //Examine all trims in the input foreach( BrepTrim trim in srf.Trims) { //Nada edge of a trim indicates a singularity if( trim.Edge == aught) { //Find the 2nd parameter infinite point of the start or end of the trim Point2d pt2d = new Point2d(trim.PointAtStart); //Evaluate trim end point on the object surface Point3d pt3d = trim.Face up.PointAt(pt2d.Ten, pt2d.Y); //Add 3D point to the list of singular points singular_points.Add(pt3d); } } //Asign output A = singular_points } Download Sample Files
Download the math-samplesandtutorials.zero archive, containing all the example Grasshopper and code files in this guide.
Next Steps
If you would like to inquiry more, bank check out the References guide to learn more about the detailed structure of NURBS curves and surfaces.
Source: https://developer.rhino3d.com/guides/general/essential-mathematics/parametric-curves-surfaces/
0 Response to "draw tangent with curve civil 3d"
Enregistrer un commentaire